Linear regression - OLS Model¶
In this section, we will cover:
fitting an OLS linear regression model
score analysis: MSE and variance explained: \(R^2\)
residual analysis
[1]:
import pandas as pd
import numpy as np
import pickle
import time
[2]:
df = pd.read_csv('data/df_resample.csv')
df.head()
[2]:
| symboling | make | fuel_type | aspiration | num_of_doors | body_style | drive_wheels | engine_location | wheel_base | length | ... | engine_size | fuel_system | bore | stroke | compression_ratio | horsepower | peak_rpm | city_mpg | highway_mpg | price | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | nissan | gas | std | four | sedan | fwd | front | 97.2 | 173.4 | ... | 120 | 2bbl | 3.33 | 3.47 | 8.5 | 97.0 | 5200.0 | 27 | 34 | 9549.0 |
| 1 | 3 | volkswagen | gas | std | two | hatchback | fwd | front | 94.5 | 165.7 | ... | 109 | mpfi | 3.19 | 3.40 | 8.5 | 90.0 | 5500.0 | 24 | 29 | 9980.0 |
| 2 | 1 | bmw | gas | std | four | sedan | rwd | front | 103.5 | 189.0 | ... | 164 | mpfi | 3.31 | 3.19 | 9.0 | 121.0 | 4250.0 | 20 | 25 | 24565.0 |
| 3 | 2 | subaru | gas | std | two | hatchback | fwd | front | 93.7 | 156.9 | ... | 97 | 2bbl | 3.62 | 2.36 | 9.0 | 69.0 | 4900.0 | 31 | 36 | 5118.0 |
| 4 | 0 | mazda | diesel | std | four | sedan | rwd | front | 104.9 | 175.0 | ... | 134 | idi | 3.43 | 3.64 | 22.0 | 72.0 | 4200.0 | 31 | 39 | 18344.0 |
5 rows × 25 columns
[3]:
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 10000 entries, 0 to 9999
Data columns (total 25 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 symboling 10000 non-null int64
1 make 10000 non-null object
2 fuel_type 10000 non-null object
3 aspiration 10000 non-null object
4 num_of_doors 10000 non-null object
5 body_style 10000 non-null object
6 drive_wheels 10000 non-null object
7 engine_location 10000 non-null object
8 wheel_base 10000 non-null float64
9 length 10000 non-null float64
10 width 10000 non-null float64
11 height 10000 non-null float64
12 curb_weight 10000 non-null int64
13 engine_type 10000 non-null object
14 num_of_cylinders 10000 non-null object
15 engine_size 10000 non-null int64
16 fuel_system 10000 non-null object
17 bore 10000 non-null float64
18 stroke 10000 non-null float64
19 compression_ratio 10000 non-null float64
20 horsepower 10000 non-null float64
21 peak_rpm 10000 non-null float64
22 city_mpg 10000 non-null int64
23 highway_mpg 10000 non-null int64
24 price 10000 non-null float64
dtypes: float64(10), int64(5), object(10)
memory usage: 1.9+ MB
Train-test split¶
To avoid overfitting, we will split our data on train and test sets.
The model will be trained with the train dataset and later we will evaluate it with the test set.
[4]:
from sklearn.model_selection import train_test_split
X = df.copy()
X.drop('price', axis=1, inplace=True)
y = np.log(df.price) # as discussed, we are going to use the log transformation here
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=.3, random_state=95276
)
Feature Selection¶
It is very important to carefully chose which features will be included into the model, because:
including unnecessary features increases the standard error of the coefficients
excluding necessary features results in bias
Selection through correlation¶
As we want start trying out linear regression models, we will select features that have linear correlation with the dependent variable price.
[5]:
# categorical features
with open('data/category_list', 'rb') as file:
cat_cols = pickle.load(file)
# numeric columns
num_cols = [col for col in X_train.columns if col not in cat_cols]
num_cols
[5]:
['wheel_base',
'length',
'width',
'height',
'curb_weight',
'engine_size',
'bore',
'stroke',
'compression_ratio',
'horsepower',
'peak_rpm',
'city_mpg',
'highway_mpg']
[6]:
X_train['price'] = y_train
cols = num_cols + ['price']
cor = X_train[cols].corr().abs()
cor.loc[cor.price > .5, 'price'].sort_values()
C:\Users\BJ571WQ\Anaconda3\lib\site-packages\ipykernel_launcher.py:1: SettingWithCopyWarning:
A value is trying to be set on a copy of a slice from a DataFrame.
Try using .loc[row_indexer,col_indexer] = value instead
See the caveats in the documentation: https://pandas.pydata.org/pandas-docs/stable/user_guide/indexing.html#returning-a-view-versus-a-copy
"""Entry point for launching an IPython kernel.
[6]:
bore 0.590618
wheel_base 0.637270
length 0.780432
city_mpg 0.785230
highway_mpg 0.788294
width 0.803110
horsepower 0.827188
engine_size 0.844736
curb_weight 0.895085
price 1.000000
Name: price, dtype: float64
[7]:
mask = (cor.price > .5 ) & (cor.price < 1)
correlated = cor[mask].sort_values(by='price').index
not_correlated = [col for col in num_cols if col not in correlated]
print('correlated: ', correlated)
print('not correlated: ', not_correlated)
correlated: Index(['bore', 'wheel_base', 'length', 'city_mpg', 'highway_mpg', 'width',
'horsepower', 'engine_size', 'curb_weight'],
dtype='object')
not correlated: ['height', 'stroke', 'compression_ratio', 'peak_rpm']
Fitting the model¶
Formula for OLS¶
[8]:
cat_list = [f'C({cat})' for cat in cat_cols]
cat_formula = ' + '.join(cat_list)
num_formula = ' + '.join(correlated)
formula = f'price ~ {cat_formula} + {num_formula}'
formula
[8]:
'price ~ C(make) + C(fuel_type) + C(aspiration) + C(num_of_doors) + C(body_style) + C(drive_wheels) + C(engine_location) + C(engine_type) + C(num_of_cylinders) + C(fuel_system) + C(symboling) + bore + wheel_base + length + city_mpg + highway_mpg + width + horsepower + engine_size + curb_weight'
[9]:
import statsmodels.formula.api as smf
model = smf.ols(formula=formula, data=X_train)
res = model.fit()
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.969
Model: OLS Adj. R-squared: 0.969
Method: Least Squares F-statistic: 3976.
Date: Tue, 08 Sep 2020 Prob (F-statistic): 0.00
Time: 16:41:56 Log-Likelihood: 7096.2
No. Observations: 7000 AIC: -1.408e+04
Df Residuals: 6944 BIC: -1.370e+04
Df Model: 55
Covariance Type: nonrobust
=================================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------------
Intercept 4.7194 0.071 66.565 0.000 4.580 4.858
C(make)[T.audi] 0.3223 0.019 16.807 0.000 0.285 0.360
C(make)[T.bmw] 0.3656 0.018 20.808 0.000 0.331 0.400
C(make)[T.chevrolet] -0.0854 0.018 -4.718 0.000 -0.121 -0.050
C(make)[T.dodge] -0.1320 0.014 -9.546 0.000 -0.159 -0.105
C(make)[T.honda] 0.1660 0.017 9.787 0.000 0.133 0.199
C(make)[T.isuzu] -0.4436 0.020 -22.238 0.000 -0.483 -0.405
C(make)[T.jaguar] -0.1599 0.021 -7.591 0.000 -0.201 -0.119
C(make)[T.mazda] -0.0011 0.014 -0.084 0.933 -0.028 0.025
C(make)[T.mercedes-benz] -0.0189 0.020 -0.942 0.346 -0.058 0.020
C(make)[T.mercury] -0.0778 0.023 -3.320 0.001 -0.124 -0.032
C(make)[T.mitsubishi] -0.1376 0.014 -9.711 0.000 -0.165 -0.110
C(make)[T.nissan] 0.0138 0.013 1.062 0.288 -0.012 0.039
C(make)[T.peugot] -0.2821 0.016 -18.150 0.000 -0.313 -0.252
C(make)[T.plymouth] -0.1657 0.014 -12.015 0.000 -0.193 -0.139
C(make)[T.porsche] 0.3364 0.022 14.997 0.000 0.292 0.380
C(make)[T.saab] 0.1741 0.016 10.705 0.000 0.142 0.206
C(make)[T.subaru] -0.1974 0.013 -14.770 0.000 -0.224 -0.171
C(make)[T.toyota] -0.1405 0.013 -11.237 0.000 -0.165 -0.116
C(make)[T.volkswagen] -0.0154 0.014 -1.066 0.286 -0.044 0.013
C(make)[T.volvo] -0.0357 0.016 -2.168 0.030 -0.068 -0.003
C(fuel_type)[T.gas] 2.2407 0.035 63.510 0.000 2.172 2.310
C(aspiration)[T.turbo] 0.1349 0.006 21.058 0.000 0.122 0.147
C(num_of_doors)[T.two] -0.0474 0.004 -10.734 0.000 -0.056 -0.039
C(body_style)[T.hardtop] -0.1464 0.010 -14.358 0.000 -0.166 -0.126
C(body_style)[T.hatchback] -0.1858 0.009 -20.640 0.000 -0.203 -0.168
C(body_style)[T.sedan] -0.1872 0.010 -19.010 0.000 -0.207 -0.168
C(body_style)[T.wagon] -0.2630 0.010 -25.327 0.000 -0.283 -0.243
C(drive_wheels)[T.rwd] 0.1927 0.007 29.121 0.000 0.180 0.206
C(engine_location)[T.rear] 0.2984 0.016 18.586 0.000 0.267 0.330
C(engine_type)[T.l] -0.1144 0.014 -8.401 0.000 -0.141 -0.088
C(engine_type)[T.ohc] -0.0648 0.009 -7.108 0.000 -0.083 -0.047
C(engine_type)[T.ohcf] 0.1011 0.008 12.244 0.000 0.085 0.117
C(engine_type)[T.ohcv] -0.1056 0.011 -10.014 0.000 -0.126 -0.085
C(num_of_cylinders)[T.five] -0.1452 0.024 -6.137 0.000 -0.192 -0.099
C(num_of_cylinders)[T.four] -0.0754 0.029 -2.586 0.010 -0.133 -0.018
C(num_of_cylinders)[T.six] -0.1888 0.022 -8.633 0.000 -0.232 -0.146
C(num_of_cylinders)[T.three] 0.1677 0.024 6.972 0.000 0.121 0.215
C(num_of_cylinders)[T.twelve] -0.0545 0.030 -1.803 0.071 -0.114 0.005
C(fuel_system)[T.2bbl] 0.2087 0.012 17.444 0.000 0.185 0.232
C(fuel_system)[T.idi] 2.4787 0.037 67.266 0.000 2.406 2.551
C(fuel_system)[T.mfi] 0.2890 0.022 13.203 0.000 0.246 0.332
C(fuel_system)[T.mpfi] 0.2880 0.012 23.062 0.000 0.263 0.312
C(fuel_system)[T.spdi] 0.2471 0.015 16.480 0.000 0.218 0.276
C(fuel_system)[T.spfi] 0.5898 0.025 23.329 0.000 0.540 0.639
C(symboling)[T.-1] 0.1008 0.011 9.326 0.000 0.080 0.122
C(symboling)[T.0] 0.1112 0.012 9.220 0.000 0.088 0.135
C(symboling)[T.1] 0.0327 0.013 2.581 0.010 0.008 0.058
C(symboling)[T.2] 2.929e-05 0.013 0.002 0.998 -0.026 0.026
C(symboling)[T.3] 0.0828 0.014 5.826 0.000 0.055 0.111
bore -0.1834 0.015 -12.535 0.000 -0.212 -0.155
wheel_base 0.0084 0.001 11.295 0.000 0.007 0.010
length -0.0045 0.000 -10.618 0.000 -0.005 -0.004
city_mpg -0.0178 0.001 -15.892 0.000 -0.020 -0.016
highway_mpg 0.0131 0.001 13.579 0.000 0.011 0.015
width 0.0231 0.002 11.809 0.000 0.019 0.027
horsepower -0.0002 0.000 -0.887 0.375 -0.001 0.000
engine_size 0.0022 0.000 10.676 0.000 0.002 0.003
curb_weight 0.0005 1.25e-05 37.256 0.000 0.000 0.000
==============================================================================
Omnibus: 5.085 Durbin-Watson: 1.999
Prob(Omnibus): 0.079 Jarque-Bera (JB): 5.197
Skew: -0.044 Prob(JB): 0.0744
Kurtosis: 3.100 Cond. No. 1.02e+16
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 4.65e-22. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
More feature selection: p-values¶
When we fit a linear regression model, we have to test the hypothesis that the evaluated coefficient for a given regressor is actually zero, meaning we don’t need that regressor at all.
In other words, we have:
\(H_0\): the coefficient is zero
\(H_1\): the coefficient is not zero
Therefore, let’s look into the p-values for each coefficient for each regressor to understand if they should be zero:
if a p-value of a given coefficient is larger than 5%, then we fail to reject the null hypothesis that the coefficient actually is zero
[10]:
res.pvalues[res.pvalues > .05]
# we are not taking out make just because a few rotten apples
[10]:
C(make)[T.mazda] 0.932911
C(make)[T.mercedes-benz] 0.346465
C(make)[T.nissan] 0.288217
C(make)[T.volkswagen] 0.286270
C(num_of_cylinders)[T.twelve] 0.071427
C(symboling)[T.2] 0.998247
horsepower 0.375116
dtype: float64
As we can see, the p-values for some makers are larger than 5%. We are not removing this feature.
On the other hand, hypothesis testing for variable horsepower coefficient shows it could be zero.
Therefore, lets remove this feature and fit the model again:
[11]:
correlated = correlated.tolist()
correlated.remove('horsepower')
num_formula = ' + '.join(correlated)
formula = f'price ~ {cat_formula} + {num_formula}'
start = time.time()
model = smf.ols(formula=formula, data=X_train)
res = model.fit()
stop = time.time()
elapsed = stop - start
print(res.summary())
OLS Regression Results
==============================================================================
Dep. Variable: price R-squared: 0.969
Model: OLS Adj. R-squared: 0.969
Method: Least Squares F-statistic: 4050.
Date: Tue, 08 Sep 2020 Prob (F-statistic): 0.00
Time: 16:41:57 Log-Likelihood: 7095.8
No. Observations: 7000 AIC: -1.408e+04
Df Residuals: 6945 BIC: -1.370e+04
Df Model: 54
Covariance Type: nonrobust
=================================================================================================
coef std err t P>|t| [0.025 0.975]
-------------------------------------------------------------------------------------------------
Intercept 4.7214 0.071 66.632 0.000 4.583 4.860
C(make)[T.audi] 0.3190 0.019 16.970 0.000 0.282 0.356
C(make)[T.bmw] 0.3628 0.017 20.991 0.000 0.329 0.397
C(make)[T.chevrolet] -0.0893 0.018 -5.095 0.000 -0.124 -0.055
C(make)[T.dodge] -0.1344 0.014 -9.895 0.000 -0.161 -0.108
C(make)[T.honda] 0.1620 0.016 9.903 0.000 0.130 0.194
C(make)[T.isuzu] -0.4441 0.020 -22.269 0.000 -0.483 -0.405
C(make)[T.jaguar] -0.1556 0.021 -7.591 0.000 -0.196 -0.115
C(make)[T.mazda] -0.0030 0.013 -0.227 0.821 -0.029 0.023
C(make)[T.mercedes-benz] -0.0196 0.020 -0.980 0.327 -0.059 0.020
C(make)[T.mercury] -0.0852 0.022 -3.889 0.000 -0.128 -0.042
C(make)[T.mitsubishi] -0.1401 0.014 -10.097 0.000 -0.167 -0.113
C(make)[T.nissan] 0.0110 0.013 0.869 0.385 -0.014 0.036
C(make)[T.peugot] -0.2786 0.015 -18.557 0.000 -0.308 -0.249
C(make)[T.plymouth] -0.1678 0.014 -12.348 0.000 -0.194 -0.141
C(make)[T.porsche] 0.3321 0.022 15.155 0.000 0.289 0.375
C(make)[T.saab] 0.1705 0.016 10.833 0.000 0.140 0.201
C(make)[T.subaru] -0.1956 0.013 -14.798 0.000 -0.222 -0.170
C(make)[T.toyota] -0.1422 0.012 -11.502 0.000 -0.166 -0.118
C(make)[T.volkswagen] -0.0176 0.014 -1.236 0.217 -0.046 0.010
C(make)[T.volvo] -0.0372 0.016 -2.277 0.023 -0.069 -0.005
C(fuel_type)[T.gas] 2.2405 0.035 63.507 0.000 2.171 2.310
C(aspiration)[T.turbo] 0.1312 0.005 26.932 0.000 0.122 0.141
C(num_of_doors)[T.two] -0.0475 0.004 -10.755 0.000 -0.056 -0.039
C(body_style)[T.hardtop] -0.1471 0.010 -14.469 0.000 -0.167 -0.127
C(body_style)[T.hatchback] -0.1869 0.009 -20.948 0.000 -0.204 -0.169
C(body_style)[T.sedan] -0.1883 0.010 -19.255 0.000 -0.207 -0.169
C(body_style)[T.wagon] -0.2639 0.010 -25.553 0.000 -0.284 -0.244
C(drive_wheels)[T.rwd] 0.1912 0.006 29.961 0.000 0.179 0.204
C(engine_location)[T.rear] 0.2957 0.016 18.758 0.000 0.265 0.327
C(engine_type)[T.l] -0.1142 0.014 -8.387 0.000 -0.141 -0.088
C(engine_type)[T.ohc] -0.0610 0.008 -7.567 0.000 -0.077 -0.045
C(engine_type)[T.ohcf] 0.1001 0.008 12.235 0.000 0.084 0.116
C(engine_type)[T.ohcv] -0.1038 0.010 -10.035 0.000 -0.124 -0.084
C(num_of_cylinders)[T.five] -0.1495 0.023 -6.460 0.000 -0.195 -0.104
C(num_of_cylinders)[T.four] -0.0816 0.028 -2.880 0.004 -0.137 -0.026
C(num_of_cylinders)[T.six] -0.1940 0.021 -9.207 0.000 -0.235 -0.153
C(num_of_cylinders)[T.three] 0.1644 0.024 6.919 0.000 0.118 0.211
C(num_of_cylinders)[T.twelve] -0.0667 0.027 -2.471 0.013 -0.120 -0.014
C(fuel_system)[T.2bbl] 0.2077 0.012 17.438 0.000 0.184 0.231
C(fuel_system)[T.idi] 2.4809 0.037 67.489 0.000 2.409 2.553
C(fuel_system)[T.mfi] 0.2865 0.022 13.199 0.000 0.244 0.329
C(fuel_system)[T.mpfi] 0.2854 0.012 23.486 0.000 0.262 0.309
C(fuel_system)[T.spdi] 0.2449 0.015 16.551 0.000 0.216 0.274
C(fuel_system)[T.spfi] 0.5884 0.025 23.320 0.000 0.539 0.638
C(symboling)[T.-1] 0.1024 0.011 9.598 0.000 0.081 0.123
C(symboling)[T.0] 0.1131 0.012 9.544 0.000 0.090 0.136
C(symboling)[T.1] 0.0352 0.012 2.839 0.005 0.011 0.059
C(symboling)[T.2] 0.0023 0.013 0.179 0.858 -0.023 0.028
C(symboling)[T.3] 0.0857 0.014 6.180 0.000 0.058 0.113
bore -0.1812 0.014 -12.565 0.000 -0.210 -0.153
wheel_base 0.0085 0.001 11.698 0.000 0.007 0.010
length -0.0045 0.000 -10.611 0.000 -0.005 -0.004
city_mpg -0.0176 0.001 -16.130 0.000 -0.020 -0.015
highway_mpg 0.0130 0.001 13.570 0.000 0.011 0.015
width 0.0228 0.002 11.846 0.000 0.019 0.027
engine_size 0.0021 0.000 11.974 0.000 0.002 0.002
curb_weight 0.0005 1.25e-05 37.323 0.000 0.000 0.000
==============================================================================
Omnibus: 4.426 Durbin-Watson: 1.999
Prob(Omnibus): 0.109 Jarque-Bera (JB): 4.512
Skew: -0.040 Prob(JB): 0.105
Kurtosis: 3.095 Cond. No. 1.02e+16
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The smallest eigenvalue is 4.64e-22. This might indicate that there are
strong multicollinearity problems or that the design matrix is singular.
[12]:
res.pvalues[res.pvalues > .05]
[12]:
C(make)[T.mazda] 0.820602
C(make)[T.mercedes-benz] 0.327119
C(make)[T.nissan] 0.385010
C(make)[T.volkswagen] 0.216545
C(symboling)[T.2] 0.857865
dtype: float64
Now we are done with feature selection.
Model Scoring & Evaluation¶
[13]:
r2 = res.rsquared_adj
predictions = np.exp(res.predict(X_test)) # back transformation
mse = np.mean(
(predictions - np.exp(y_test))**2
)
print(f'R^2: {r2:.4}')
print(f'MSE: {mse:.4}')
R^2: 0.969
MSE: 2.175e+06
[14]:
data = {
'model name': ['ols'],
'r2': [r2],
'MSE': [mse],
'time': elapsed
}
score_df = pd.DataFrame(data)
score_df.to_csv('data/scores.csv', index=False)
score_df
[14]:
| model name | r2 | MSE | time | |
|---|---|---|---|---|
| 0 | ols | 0.968982 | 2.175057e+06 | 0.363137 |
Residual analysis¶
In a good model, we should expect that the residuals:
have mean zero
to be homoscedastic
to be normal
to have no correlation with the fitted values
to have no correlation with any of the features
Residuals vs fitted values¶
[16]:
from numpy.polynomial.polynomial import polyfit
import matplotlib.pyplot as plt
%matplotlib inline
plt.figure(figsize=(12, 5))
plt.title('fitted price vs resids')
plt.scatter(res.fittedvalues, res.resid, c="g", alpha=0.5, label="OLS model")
b, m = polyfit(res.fittedvalues, res.resid, 1)
plt.plot(res.fittedvalues, b + m * res.fittedvalues, '-')
plt.xlabel("")
plt.ylabel("")
plt.legend(loc=2)
[16]:
<matplotlib.legend.Legend at 0x27afa2eeac8>
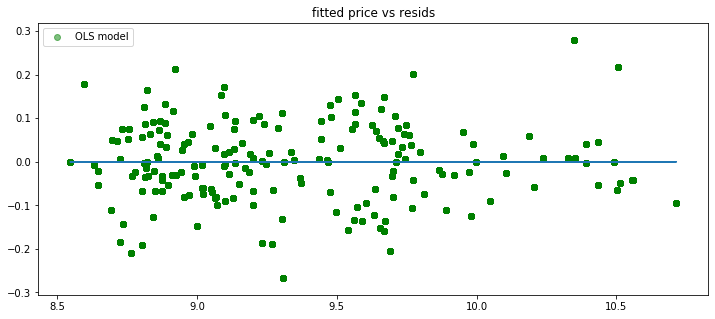
Correlation between residuals and \(\hat y\)¶
In a good model, residuals cannot be correlated to the fitted values.
[17]:
from scipy.stats.stats import pearsonr
pearsonr(res.predict(X_train), res.resid)
[17]:
(8.134968393358477e-13, 0.9999999999497379)
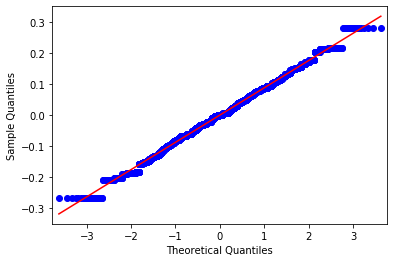
Test for normality¶
[18]:
import scipy.stats as st
st.shapiro(res.resid)
C:\Users\BJ571WQ\Anaconda3\lib\site-packages\scipy\stats\morestats.py:1676: UserWarning: p-value may not be accurate for N > 5000.
warnings.warn("p-value may not be accurate for N > 5000.")
[18]:
(0.9971299767494202, 2.398374832068839e-10)
[19]:
from statsmodels.graphics.gofplots import qqplot
qqplot(res.resid, line='s');